Evaluating cotan

Given two vectors in , and , how do we evaluate the cotangent of the angle between these vectors?

We could do this explicitly, by using inverse trig functions to find the angle between the vectors, then taking the cotangent of that angle. However, with some derivation we can find an alternate approach, which is simpler, more efficient, and more numerically robust.

Of course, the cotangent is given by

Recall that the dot product is given by . The magnitude of the cross product is given by . We can use these to evaluate !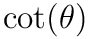

This "dot over cross" expression is thus equivalent to the cotangent of the angle, yet does not require evaluating any trig functions. It also avoids having to normalize the vectors.