How to Optimize a Continuous Function

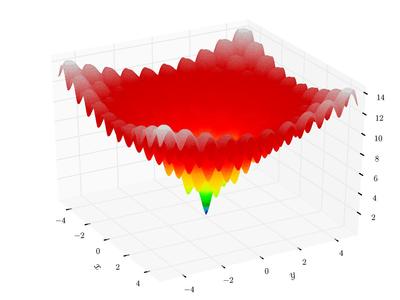
In mathematical optimization, the Ackley function, which has many local minima, is a non-convex function used as a performance test problem for optimization algorithms. In 2-dimension, it looks like (from wikipedia)

We define the Ackley function in simple_function.py for minimization

import numpy as np

def ackley(solution):
    """
    Ackley function for continuous optimization
    """
    x = solution.get_x()
    bias = 0.2
    ave_seq = sum([(i - bias) * (i - bias) for i in x]) / len(x)
    ave_cos = sum([np.cos(2.0*np.pi*(i-bias)) for i in x]) / len(x)
    value = -20 * np.exp(-0.2 * np.sqrt(ave_seq)) - np.exp(ave_cos) + 20.0 + np.e
    return value

Then, define corresponding objective and parameter.

dim_size = 100  # dimensions
dim_regs = [[-1, 1]] * dim_size  # dimension range
dim_tys = [True] * dim_size  # dimension type : real
dim = Dimension(dim_size, dim_regs, dim_tys)  # form up the dimension object
objective = Objective(ackley, dim)  # form up the objective function

budget = 100 * dim_size  # number of calls to the objective function
parameter = Parameter(budget=budget)

Finally, optimize this function.

solution_list = ExpOpt.min(objective, parameter, repeat=1, plot=True)

The whole process lists below.

from simple_function import ackley
from zoopt import Dimension, Objective, Parameter, ExpOpt


def minimize_ackley_continuous():
    """
    Continuous optimization example of minimizing the ackley function.

    :return: no return value
    """
    dim_size = 100  # dimensions
    dim_regs = [[-1, 1]] * dim_size  # dimension range
    dim_tys = [True] * dim_size  # dimension type : real
    dim = Dimension(dim_size, dim_regs, dim_tys)  # form up the dimension object
    objective = Objective(ackley, dim)  # form up the objective function

    budget = 100 * dim_size  # number of calls to the objective function
    parameter = Parameter(budget=budget)

    solution_list = ExpOpt.min(objective, parameter, repeat=1, plot=True)
    
if __name__ == '__main__':
    minimize_ackley_continuous()

For a few seconds, the optimization is done. Visualized optimization progress looks like

More concrete examples are available in the example/simple_functions/continuous_opt.py file .