-
Notifications
You must be signed in to change notification settings - Fork 30
1D Euler equations
The 1D Euler equations is a non linear system of Partial Differential Equations (PDE). The Euler system describes the dynamics of compressible flows for which the effects of body forces, viscous stress and heat fluxes can be neglected. It is commonly used for describing compressible gas dynamics of high-velocity flows, see [].
The 1D Euler PDEs system for and ideal flow can be written as:
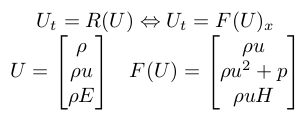
where r is the density, u is the velocity, p the pressure, E the total internal specific energy and H the total specific enthalpy. The PDEs system must completed with the proper initial and boundary conditions. Moreover, an ideal (thermally and calorically perfect) gas is considered
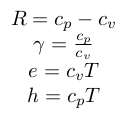
where R is the gas constant, cp cv are the specific heats at constant pressure and volume (respectively), e is the internal energy, h is the internal enthalpy and T is the temperature. The following additionally equations of state hold:
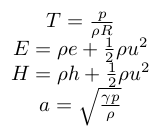
An extension of the above Euler's system is considered allowing the modelling of a multi-fluid mixture of different gas (with different physical characteristics). The well known Standard Thermodynamic Model is used to model the gas mixture replacing the density with the density fraction of each specie composing the mixture. This led to the following system:
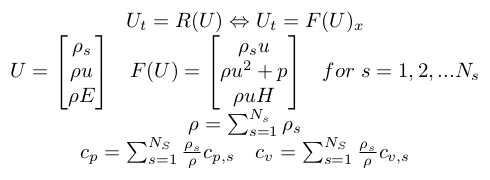
where Ns is the number of initial species composing the gas mixture.
The Euler's conservation laws are non linear, unsteady, hyperbolic PDEs system that admits discontinuous solutions (contact/material discontinuities and shocks). The integration of this system requires accurate time-space numerical integration schemes: in order to easily capture discontinuous solutions a fully conservative scheme is the preferred approach where the generation of non-physical oscillations (time-space generation of Gibb's phenomenon, see []) must be accurately controlled.
Here we are focused on the time integration aspect, thus the discretization of the space operator (that eventually lead to the algebraic ODEs sytem) is only breafly described.
For the above reasons, the 1D Euler system constitutes a valuable benchmark for FOODIE library retaining many complex aspects while it being yet simple enough to be accurately controlled.
It has been chosen to adopt a finite volume, fully conservative, Godunov-like numerical scheme. Here the residual function of the 1D Euler system involves the computations (at each time step) of the cell-interfaces fluxes. The computation of the inter-cell fluxes is essentially the resolution of a Riemann Problem. The Local-Lax-Friedrichs (or Rusanov) scheme is here employed, see []. For the coupling with high order time integration schemes, a WENO upwind-biased scheme is also employed, see []. The boundary conditions imposition is based on the ghost-cell approach where the actual space-domain is enlarged by a frame of cells (the ghost ones) the flow-field values of which are imposed (at each time step) in order to obtain the correct interface fluxes at the domain boundaries.
It is worth to note that due to the unsteady non-linear character and discontinuity solutions presence, the space operator should have the Total Variation Diminishing (TVD) property or at least the Essentially Non-Oscillatory one. This is also true for the time integrator.
[1] Numerical Methods for Fluid Dynamics With Applications to Geophysics, Dale R. Durran, Springer, 2010.
Before apply a FOODIE solver for solving the above system the system itself must be defined accordingly to FOODIE's type_integrand abstract type (upon which each FOODIE's solver is based).
The proposed FOODIE-compatible 1D Euler's system definition is:
type, extends(integrand) :: euler_1D
!< Euler 1D PDEs system field.
!<
!< It is a FOODIE integrand class.
private
integer(I_P) :: steps=0 !< Number of time steps stored.
integer(I_P) :: ord=0 !< Space accuracy formal order.
integer(I_P) :: Ni=0 !< Space dimension.
integer(I_P) :: Ng=0 !< Number of ghost cells for boundary conditions handling.
integer(I_P) :: Ns=0 !< Number of initial species.
integer(I_P) :: Nc=0 !< Number of conservative variables, Ns+2.
integer(I_P) :: Np=0 !< Number of primitive variables, Ns+4.
real(R_P) :: Dx=0._R_P !< Space step.
real(R_P), allocatable :: U(:,:) !< Conservative (state) variables [1:Nc,1-Ng:Ni+Ng].
real(R_P), allocatable :: previous(:,:,:) !< Conservative (state) variables of previous time steps [1:Nc,1-Ng:Ni+Ng,1:steps].
real(R_P), allocatable :: cp0(:) !< Specific heat cp of initial species [1:Ns].
real(R_P), allocatable :: cv0(:) !< Specific heat cv of initial species [1:Ns].
character(:), allocatable :: BC_L !< Left boundary condition type.
character(:), allocatable :: BC_R !< Right boundary condition type.
contains
! public methods
! auxiliary methods
procedure, pass(self), public :: init !< Init field.
procedure, pass(self), public :: destroy !< Destroy field.
procedure, pass(self), public :: output !< Extract Euler field.
procedure, pass(self), public :: dt => compute_dt !< Compute the current time step, by means of CFL condition.
! type_integrand deferred methods
procedure, pass(self), public :: t => dEuler_dt !< Time derivate, residuals function.
procedure, pass(self), public :: update_previous_steps !< Update previous time steps.
! operators overloading
procedure, pass(lhs), public :: integrand_multiply_integrand => euler_multiply_euler !< Euler * Euler operator.
procedure, pass(lhs), public :: integrand_multiply_real => euler_multiply_real !< Euler * real operator.
procedure, pass(rhs), public :: real_multiply_integrand => real_multiply_euler !< Real * Euler operator.
procedure, pass(lhs), public :: add => add_euler !< Euler + Euler oprator.
procedure, pass(lhs), public :: assign_integrand => euler_assign_euler !< Euler = Euler.
procedure, pass(lhs), public :: assign_real => euler_assign_real !< Euler = real.
! private methods
procedure, pass(self), private :: primitive2conservative !< Convert primitive variables to conservative ones.
procedure, pass(self), private :: conservative2primitive !< Convert conservative variables to primitive ones.
procedure, pass(self), private :: impose_boundary_conditions !< Impose boundary conditions.
procedure, pass(self), private :: reconstruct_interfaces_states !< Reconstruct interfaces states.
procedure, pass(self), private :: riemann_solver !< Solve the Riemann Problem at cell interfaces.
final :: finalize !< Finalize field.
endtype euler_1DThis Euler type embeds:
- some parameters values (mainly for handling the space domain);
- the Euler's U conservative state variable vector;
- 3 auxiliary (helper) methods, not detailed here they being of minor interest;
- all the
type_integranddeferred methods that are necessary for the definition of a valid concrete extension oftype_integrand.
We chose to define the Oscillation' state vector as a rank 2 array: it is a map of whole space domain where in the first subscript there is the conservative state variables while in the second there is cell-centered space location. The actual meaning of each conservative state variables can be found directly into the source doc-strings.
The time derivative method euler_1D%t => deuler_1D_dt, namely the residuals function, depends on the state vector and on the space location at time step considered, thus we must transform the PDEs system to an algebraic ODEs one. As stated above this involves the computation of the Riemann Problem solution at each inter-cell interface.
Using the above euler_1D type definition it simply corresponds to:
function dEuler_dt(self, n) result(dState_dt)
!---------------------------------------------------------------------------------------------------------------------------------
!< Time derivative of Euler field, the residuals function.
!---------------------------------------------------------------------------------------------------------------------------------
class(euler_1D), intent(IN) :: self !< Euler field.
integer(I_P), optional, intent(IN) :: n !< Time level.
class(integrand), allocatable :: dState_dt !< Euler field time derivative.
real(R_P), allocatable :: F(:,:) !< Fluxes of conservative variables.
real(R_P), allocatable :: P(:,:) !< Primitive variables.
real(R_P), allocatable :: PR(:,:,:) !< Left (1) and right (2) (reconstructed) interface values of primitive variables.
integer(I_P) :: dn !< Time level, dummy variable.
integer(I_P) :: i !< Counter.
!---------------------------------------------------------------------------------------------------------------------------------
!---------------------------------------------------------------------------------------------------------------------------------
associate (Ni=>self%Ni, Ng=>self%Ng, Nc=>self%Nc, Np=>self%Np, Ns=>self%Ns, U=>self%U, previous=>self%previous)
! allocate temporary arrays
allocate(F(1:Nc, 0:Ni)) ; F = 0._R_P
allocate(P(1:Np, 1-Ng:Ni+Ng)) ; P = 0._R_P
allocate(PR(1:Np, 1:2, 0:Ni+1)) ; PR = 0._R_P
! compute primitive variables
if (self%steps>=2) then ! self%previous should be used, multi-step time integration
dn = self%steps ; if (present(n)) dn = n
do i=1, Ni
P(:, i) = self%conservative2primitive(previous(:, i, dn))
enddo
else ! self%U should be used, single-step time integration
do i=1, Ni
P(:, i) = self%conservative2primitive(U(:, i))
enddo
endif
call self%impose_boundary_conditions(primitive=P)
call self%reconstruct_interfaces_states(primitive=P, r_primitive=PR)
! compute fluxes by solving Rimeann Problems at each interface
do i=0, Ni
call self%riemann_solver(r1=PR(Ns+3, 2, i ), u1=PR(Ns+1, 2, i ), p1=PR(Ns+2, 2, i ), g1=PR(Ns+4, 2, i ), &
r4=PR(Ns+3, 1, i+1), u4=PR(Ns+1, 1, i+1), p4=PR(Ns+2, 1, i+1), g4=PR(Ns+4, 1, i+1), &
F=F(:, i))
enddo
! compute residuals
allocate(euler_1D :: dState_dt)
select type(dState_dt)
class is(euler_1D)
dState_dt = self
do i=1, Ni
dState_dt%U(:, i) = (F(:, i - 1) - F(:, i)) / self%Dx
enddo
endselect
endassociate
return
!---------------------------------------------------------------------------------------------------------------------------------
endfunction dEuler_dtHere, the class(integrand) :: dState_dt is our residuals values that leads to an algebraic system of ODEs that can be integrated by means of FOODIE. As you can see, the residuals implementation has a very-high level syntax that is easy understand and maintain.
For multi-step (level) time solver (like the Adams-Bashforth class) it is important to provide a method for update the previous time steps solution each time the current solution is integrated over one time step.
Using the above euler_1D type definition it simply corresponds to:
pure subroutine update_previous_steps(self)
!---------------------------------------------------------------------------------------------------------------------------------
!< Update previous time steps.
!---------------------------------------------------------------------------------------------------------------------------------
class(euler_1D), intent(INOUT) :: self !< Euler field.
integer :: s !< Time steps counter.
!---------------------------------------------------------------------------------------------------------------------------------
!---------------------------------------------------------------------------------------------------------------------------------
if (self%steps>0) then
do s=1, self%steps - 1
self%previous(:, :, s) = self%previous(:, :, s + 1)
enddo
self%previous(:, :, self%steps) = self%U
endif
return
!---------------------------------------------------------------------------------------------------------------------------------
endsubroutine update_previous_stepsIt a simple round-cycle that copy the solution of step n-s+1 into the n-s index, the solution of step n-s+2 into the n-s+1 index and so on until the current step n, s being the time steps used.
In the case you plan to not used multi-step solvers this method is not used, nevertheless it must be always implemented otherwise your Oscillation' definition is not a valid extension of the abstract type type_integrand. A simple implementation could be a do nothing method:
pure subroutine update_previous_steps(self)
!---------------------------------------------------------------------------------------------------------------------------------
!< FAKE update previous time steps for only non multi-step solvers.
!---------------------------------------------------------------------------------------------------------------------------------
class(euler_1D), intent(INOUT) :: self !< Oscillation field.
!---------------------------------------------------------------------------------------------------------------------------------
!---------------------------------------------------------------------------------------------------------------------------------
return
!---------------------------------------------------------------------------------------------------------------------------------
endsubroutine update_previous_stepsODE solvers typically involve operation between your integrand field (the Euler's system here) and numbers (in general reals) and other integrand field instances. This means that you must implement an almost complete set of operators methods for performing summation, multiplication, division, etc... Here we not provide more details on these methods, the interested readers can see the tests suite sources.
Let us now assume to integrate the above Euler's system by means of the Adams-Bashforth-Schemes class of solvers. The steps to this aim are very few:
...
integer(I_P), parameter :: Ni=100 !< Number of grid cells.
integer(I_P), parameter :: Nc=3 !< Number of conservative variables.
real(R_P) :: initial_state(1:Nc,1:Ni) !< Initial state of conservative variables.
type(euler_1D) :: flow !< Oscillation field.
...
call flow%init(Ni=Ni, Ns=1, Dx=Dx, BC_L=BC_L, BC_R=BC_R, initial_state=initial_state, cp0=cp0, cv0=cv0, ord=7)The Adams-Bashforth solvers class must be initialized selecting the time steps used:
...
type(adams_bashforth_integrator) :: ab_integrator !< Adams-Bashforth integrator.
...
call ab_integrator%init(steps=3)do while(.not.finished)
...
call ab_integrator%integrate(field=flow, dt=0.01)
...
enddoFor a complete example see the Euler's test.