High Level Programming

Formula Translator

As scientist we want to translate our mathematical/numerical formula as easier as possible: Fortran is our best friend! However, until Fortran 2003/2008 standard, procedural or functional programming was the only reliable approach for Fortraners. Procedural and functional programming are not the evil, however they do not fit well if you want to have your source code to be as close as possible to your formal high-level maths language. To this purpose, Object Oriented Programming can help you to perform a quantum leap in the future!

The problem

We want to code a formula like the following

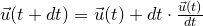
it being the forward explicit Euler integration scheme. This is probably the simplest ODE solver scheme you can devise, however the translation into an actual Fortran code can be very unclear if you use cumbersome old-style functional programming, think for example to the time-derivative function of the state vector u... On the contrary it would be very nice to translate our formula directly in Fortran with something like:

u = u + dt * u%t()

where u is a derived type (implemented by the user) that describes (with high-level language) the state vector, providing:

• its time-derivative function as a type bound procedure (u%t() means just du/dt);
• a complete set of maths operators that can be applied to it (summation u + ..., multiplication dt u%t(), etc...).

The solution

Adopt the Abstract Calculus Pattern (ACP)!

Abstract Calculus Pattern

ACP is based on the concept of Abstract Data Type (ADT, obvious!). FOODIE is based just on this concept. Essentially, all the library's schemes for solving ODE systems are expressed in very high-level language for an abstract type (the type_integrand). This ensures that:

• for ODE schemes developers:
  • work with only one, standard, derived type without the necessity to care about what the type is actually modelling (it could be the velocity field of a turbulent flow, the magnetic field of a circuit, etc...);
  • express the ODE solver formula with very high-level language; this ensures:
    • clearness!
    • fast-developing!
• for FOODIE clients:
  • a simple, standard API for many ODE solvers:
    • fast-developing of new schemes;
    • roboustness: the same ODE solver is applied to differnt problems... cross-validation;

The FOODIE Abstract Integrand Type

The definition of the FOODIE abstract integrand type is:

type, abstract :: integrand
  !< Abstract type for building FOODIE ODE integrators.
  contains
    ! public deferred procedures that concrete integrand-field must implement
    procedure(time_derivative),       pass(self), deferred, public :: t                     !< Time derivative, residuals.
    procedure(update_previous_steps), pass(self), deferred, public :: update_previous_steps !< Update the previous time steps.
    procedure(previous_step),         pass(self), deferred, public :: previous_step         !< Get a previous time step.
    ! operators
    procedure(symmetric_operator),   pass(lhs),  deferred, public :: integrand_multiply_integrand !< Integrand * integrand operator.
    procedure(integrand_op_real),    pass(lhs),  deferred, public :: integrand_multiply_real      !< Integrand * real operator.
    procedure(real_op_integrand),    pass(rhs),  deferred, public :: real_multiply_integrand      !< Real * integrand operator.
    procedure(symmetric_operator),   pass(lhs),  deferred, public :: add                          !< Integrand + integrand oprator.
    procedure(symmetric_operator),   pass(lhs),  deferred, public :: sub                          !< Integrand - integrand oprator.
    procedure(assignment_integrand), pass(lhs),  deferred, public :: assign_integrand             !< Integrand = integrand.
    procedure(assignment_real),      pass(lhs),  deferred, public :: assign_real                  !< Integrand = real.
    ! operators overloading
    generic, public :: operator(+) => add                              !< Overloading + operator.
    generic, public :: operator(-) => sub                              !< Overloading - operator.
    generic, public :: operator(*) => integrand_multiply_integrand, &
                                      real_multiply_integrand, &
                                      integrand_multiply_real          !< Overloading * operator.
    generic, public :: assignment(=) => assign_integrand, assign_real  !< Overloading = assignament.
endtype integrand

It does not implement any actual integrand field, it being and abstract type. It only specifies which deferred procedures are necessary for implementing an actual concrete integrand type. The consequences are:

• for ODE schemes developers:
  • rely only on the time-derivative function and on the operators overloaded definitions;
  • be completely agnostic on which is the actual implementation of the time-derivative residual function!
• for FOODIE clients:
  • define your concrete integrand field as an extension of this abstract type_integrand, thus you must implement all the deferred type bound procedures;
  • be completely agnostic on the actual implementation of the ODE solver you are using!

For both ODE solvers developers and FOODIE clients see the Examples & Tests.