Background and Motivations
FOODIE is designed to integrate systems of ODEs in the contest of IVPs.
The mathematical formulation of the problem is:
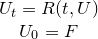
where:
- U_t = dU/dt;
- U is the vector of state variables being a function of the time-like independent variable t;
- R is the (vectorial) residual function;
- F is the (vectorial) initial conditions function.
Such a mathematical formulation is ubiquitous in the mathematical modelling of physical problems. As a matter of facts, many physical problems (fluid dynamics, chemistry, biology, evolutionary-anthropology, etc...) are described as governed by a Partial Differential Equations (PDE) system the solution of which involves the integration of above ODE system.
FOODIE is designed to be a KISS (Keep It Simple and Stupid) library for the time-like integration of the above system of ODE. In particular, FOODIE provides high-level, well-documented, simple Application Program Interface (API) for many well-known ODE integration schemes.
The web shows tons of Fortran libraries for ODE solving, thus why FOODIE? Essentially, because why not? we can... but a more conscious reason is
we would like to translate our mathematical/numerical models into computer-codes as easier as possible without compromise the computation efficiency.
The second part of the above statement (the efficiency) drives us to select Fortran as a programming language: we are scientist being not (necessarily) informatics-nerd, thus Fortran help us to translate maths in codes simply and efficiently. However, the available libraries for ODE solving are almost outdated, written in procedural/functional programming style and, in the best case, with the Fortran 95 standard. This approach limits the clearness and simplicity that we can now obtain developing a library in Fortran 2008+ standard by means of an Object Oriented Programming (OOP) approach.
We think that a modern OOP library for ODE integration can help scientist (chained to Fortran) to develop new numerical schemes faster, easier and clearer.