-
Notifications
You must be signed in to change notification settings - Fork 641
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
WIP:MaterialGrid #1242
WIP:MaterialGrid #1242
Conversation
Yes, you just mirror the block object by flipping one or more of its basis vectors. |
|
To compare errors, it might be more reliable to look at the convergence with resolution rather than the numbers at a particular resolution. |
|
I've fixed most of the gradient errors. If the two mediums in the grid are dispersionless, then the results look great: Dispersive media aren't as straightforward. If I strictly interpolate the Lorentzians (silicon and silicon dioxide in this case) without adding the conductivity damping term, the results also look good (note, I dropped the Courant factor to prevent aliasing/field instabilities): But as discussed, the conductivity factor is important to prevent instabilities as well. If I also try to interpolate the conductivity then the gradients start to fall apart: Here is a write-up that describes my implementation. I'll highlight important code pieces below. I still need to figure out why |
src/meepgeom.cpp
Outdated
| void epsilon_material_grid(material_data *md, meep::realnum u) { | ||
| // NOTE: assume p lies on normalized grid within (0,1) | ||
|
|
||
| if (!(md->design_parameters)) meep::abort("material params were not initialized!"); | ||
|
|
||
| medium_struct *mm = &(md->medium); | ||
| medium_struct *m1 = &(md->medium_1); | ||
| medium_struct *m2 = &(md->medium_2); | ||
|
|
||
| // Linearly interpolate dc epsilon values | ||
| cinterp_tensors(m1->epsilon_diag, m1->epsilon_offdiag, m2->epsilon_diag, m2->epsilon_offdiag, &mm->epsilon_diag, &mm->epsilon_offdiag, u); | ||
|
|
||
| //Interpolate resonant strength from d.p. | ||
| vector3 zero_vec; | ||
| zero_vec.x = zero_vec.y = zero_vec.z = 0; | ||
| for (int i = 0; i < m1->E_susceptibilities.num_items; i++) { | ||
| // iterate through medium1 sus list first | ||
| interp_tensors(zero_vec, zero_vec, m1->E_susceptibilities.items[i].sigma_diag, m1->E_susceptibilities.items[i].sigma_offdiag, | ||
| &mm->E_susceptibilities.items[i].sigma_diag, &mm->E_susceptibilities.items[i].sigma_offdiag, (1-u)); | ||
| } | ||
| for (int i = 0; i < m2->E_susceptibilities.num_items; i++) { | ||
| // iterate through medium2 sus list next | ||
| int j = i + m1->E_susceptibilities.num_items; | ||
| interp_tensors(zero_vec, zero_vec, m2->E_susceptibilities.items[i].sigma_diag, m2->E_susceptibilities.items[i].sigma_offdiag, | ||
| &mm->E_susceptibilities.items[j].sigma_diag, &mm->E_susceptibilities.items[j].sigma_offdiag, u); | ||
| } | ||
|
|
||
| //Linearly interpolate electric conductivity from d.p. | ||
| //This prevents instabilities when interpolating between sus. profiles. | ||
| //We assume that the material doesn't have any underlying conductance.... | ||
| if ((m1->E_susceptibilities.num_items + m2->E_susceptibilities.num_items) > 0.0) { | ||
| // calculate mean harmonic frequency | ||
| double omega_mean = 0; | ||
| for (int i = 0; i < m1->E_susceptibilities.num_items; i++) { omega_mean += m1->E_susceptibilities.items[i].frequency;} | ||
| for (int i = 0; i < m2->E_susceptibilities.num_items; i++) { omega_mean += m2->E_susceptibilities.items[i].frequency;} | ||
| omega_mean = omega_mean / (m1->E_susceptibilities.num_items + m2->E_susceptibilities.num_items); | ||
|
|
||
| // assign interpolated, nondimensionalized conductivity term | ||
| mm->D_conductivity_diag.x = mm->D_conductivity_diag.y = mm->D_conductivity_diag.z = u*(1-u) * omega_mean; | ||
| } | ||
| } |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Materials are interpolated in this function.
src/meepgeom.cpp
Outdated
| master_printf("r %g \n",temp); | ||
| return 2 * (md->medium_2.epsilon_diag.x - md->medium_1.epsilon_diag.x) * ( | ||
| (fields_a[0]*fields_f[0]).real() + (fields_a[1]*fields_f[1]).real() + (fields_a[2]*fields_f[2]).real()); | ||
| }*/ | ||
|
|
||
| // nontrivial case | ||
| std::complex<double> a[9] = {std::complex<double>(0, 0)}; | ||
| std::complex<double> dadu[9] = {std::complex<double>(0, 0)}; | ||
| std::complex<double> b[9] = {std::complex<double>(0, 0)}; | ||
| std::complex<double> dbdu[9] = {std::complex<double>(0, 0)}; | ||
|
|
||
| const medium_struct *mm = &(md->medium); | ||
| const medium_struct *m1 = &(md->medium_1); | ||
| const medium_struct *m2 = &(md->medium_2); | ||
|
|
||
| a[0] = a[4] = a[8] = std::complex<double>(1, 0); | ||
| for (int i = 0; i < 9; i++) { | ||
| // compute first part containing conductivity | ||
| // NOTE: Current implementation assumes thatmaterials being interpolated | ||
| // don't have their own conductivities! Just the synthetic conductivity | ||
| // used to dampen the interpolated lorentzians | ||
| vector3 dummy; dummy.x = dummy.y = dummy.z = 0.0; | ||
| double conductivityCur = vec_to_value(mm->D_conductivity_diag, dummy, i); | ||
| a[i] += std::complex<double>(0.0, conductivityCur / freq); | ||
|
|
||
| // compute derivative of conductivity component wrt u | ||
| if ((m1->E_susceptibilities.num_items + m2->E_susceptibilities.num_items) > 0.0) { | ||
| // calculate mean harmonic frequency | ||
| double omega_mean = 0; | ||
| for (int i = 0; i < m1->E_susceptibilities.num_items; i++) { omega_mean += m1->E_susceptibilities.items[i].frequency;} | ||
| for (int i = 0; i < m2->E_susceptibilities.num_items; i++) { omega_mean += m2->E_susceptibilities.items[i].frequency;} | ||
| omega_mean = omega_mean / (m1->E_susceptibilities.num_items + m2->E_susceptibilities.num_items); | ||
|
|
||
| // assign interpolated, nondimensionalized conductivity term to diag comps | ||
| if ((i == 0) || (i == 4) || (i==8)) dadu[i] += std::complex<double>(0.0,(1-2*u)*omega_mean/freq); | ||
| } | ||
|
|
||
| // compute lorentzian component | ||
| b[i] = cvec_to_value(mm->epsilon_diag, mm->epsilon_offdiag, i); | ||
| for (int nl = 0; nl < mm->E_susceptibilities.num_items; ++nl){ | ||
| meep::lorentzian_susceptibility sus = meep::lorentzian_susceptibility(mm->E_susceptibilities.items[nl].frequency, mm->E_susceptibilities.items[nl].gamma, mm->E_susceptibilities.items[nl].drude); | ||
| double sigma = vec_to_value(mm->E_susceptibilities.items[nl].sigma_diag, mm->E_susceptibilities.items[nl].sigma_offdiag, i); | ||
| b[i]+= sus.chi1(freq, sigma); | ||
| } | ||
|
|
||
| // compute derivative of lorentzian component wrt u | ||
| dbdu[i] = (cvec_to_value(m2->epsilon_diag, m2->epsilon_offdiag, i) - cvec_to_value(m1->epsilon_diag, m1->epsilon_offdiag, i)); | ||
| for (int nl = 0; nl < m1->E_susceptibilities.num_items; ++nl){ | ||
| meep::lorentzian_susceptibility sus = meep::lorentzian_susceptibility(m1->E_susceptibilities.items[nl].frequency, m1->E_susceptibilities.items[nl].gamma, m1->E_susceptibilities.items[nl].drude); | ||
| double sigma = vec_to_value(m1->E_susceptibilities.items[nl].sigma_diag, m1->E_susceptibilities.items[nl].sigma_offdiag, i); | ||
| dbdu[i]-= sus.chi1(freq, sigma); // subtract these ones | ||
| } | ||
| for (int nl = 0; nl < m2->E_susceptibilities.num_items; ++nl){ | ||
| meep::lorentzian_susceptibility sus = meep::lorentzian_susceptibility(m2->E_susceptibilities.items[nl].frequency, m2->E_susceptibilities.items[nl].gamma, m2->E_susceptibilities.items[nl].drude); | ||
| double sigma = vec_to_value(m2->E_susceptibilities.items[nl].sigma_diag, m2->E_susceptibilities.items[nl].sigma_offdiag, i); | ||
| dbdu[i]+= sus.chi1(freq, sigma); | ||
| } | ||
| } | ||
|
|
||
| std::complex<double> left[9] = {std::complex<double>(0,0)}; | ||
| for (int i = 0; i < 3; i++) { | ||
| for (int j = 0; j < 3; j++) { | ||
| for (int u = 0; u < 3; u++) { | ||
| int idxo = i * 3 + j; int idx1 = i * 3 + u; int idx2 = u * 3 + j; | ||
| left[idxo] += a[idx1] * dbdu[idx2]; | ||
| } | ||
| } | ||
| } | ||
|
|
||
| std::complex<double> right[9] = {std::complex<double>(0,0)}; | ||
| for (int i = 0; i < 3; i++) { | ||
| for (int j = 0; j < 3; j++) { | ||
| for (int u = 0; u < 3; u++) { | ||
| int idxo = i * 3 + j; int idx1 = i * 3 + u; int idx2 = u * 3 + j; | ||
| right[idxo] += b[idx1] * dadu[idx2]; | ||
| } | ||
| } | ||
| } | ||
|
|
||
| std::complex<double> dA_du[9] = {std::complex<double>(0,0)}; | ||
| for (int i = 0; i < 3; i++) { | ||
| for (int j = 0; j < 3; j++) { | ||
| int idx = i * 3 + j; | ||
| dA_du[idx] = left[idx] + right[idx]; | ||
| } | ||
| } | ||
|
|
||
| /*Calculate the vector-matrix-vector product conj(v1) A v2.*/ | ||
| std::complex<double> dummy[3] = {std::complex<double>(0,0)}; | ||
| // first matrix-vector product | ||
| for (int i = 0; i < 3; i++) { | ||
| for (int j = 0; j < 3; j++) { | ||
| int idx = i * 3 + j; | ||
| dummy[i] += dA_du[idx] * fields_f[j]; | ||
| } | ||
| } | ||
|
|
||
| // inner product | ||
| std::complex<double> result = dummy[0] * fields_a[0] + dummy[1] * fields_a[1] + dummy[2] * fields_a[2] ; | ||
| return 2*result.real(); |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Gradient considering material interpolation is computed here.
|
Maybe try to debug the conductivity term by itself, with no Lorentzians. |
|
All tests are passing now. After testing just the conductivity (i.e. no dispersion), I was unable to produce an accurate gradient. Consequently, I think the issue is with lossy materials in general. For now, lossy support is disabled. The user can still interpolate Lorentzians, but they better choose profiles that won't cross zero when being turned on and off (Si in the materials library should be fine, for example). Once we can figure out how to calculate the gradients with lossy materials, we can add the Lorentzian damping parameter. Note: I think this is a math issue, rather than a code issue. |
|
Ready to merge once checks pass. Note that gradients of FOM with lossy materials still don't converge. Everything else works well, however. I think the next step is to use a simpler objective function to debug (i.e. just a DFT component). The current test only checks that the You can view the updated notebooks to see how the material grid works. |
* init * basic functionality with bugs * fix boundary issues and memory leak * remove print statements * add function to update design parameters * add material sus to interpolation * add support for u_add, u_prod, etc. * init stab at gradient * fix most gradients * fix failing tests and disable conductivity * add test and update notebooks * add test to makefile * Update material_grid.py * rm matplotlib from test Co-authored-by: Alec Hammond <ahammond36@gatech.edu> Co-authored-by: Steven G. Johnson <stevenj@mit.edu>
|
|
||
| // assign interpolated, nondimensionalized conductivity term | ||
| // TODO: dampen the lorentzians to improve stability | ||
| //mm->D_conductivity_diag.x = mm->D_conductivity_diag.y = mm->D_conductivity_diag.z = u*(1-u) * omega_mean; |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
@smartalecH, I thought this had been enabled? We mention it in the paper…






closes #1199
Initial stab. The current iteration has memory leaks and struggles with dense meshes near the border of the object containing the material grid.
As of now, the user can create a
MaterialGrid(in python). The routine accepts as arguments the number of design parameters, an optional initialization array, and the twoMediumsthat are to be interpolated. The user can then assign this newMaterialGridobject to a geometry's (e.g. a block) material.Example waveguides:
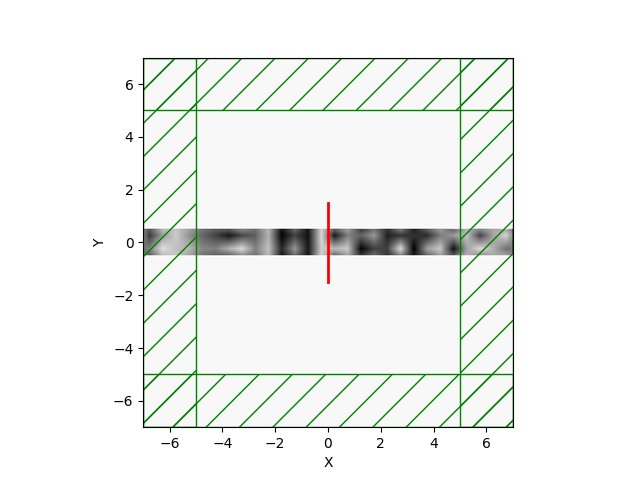
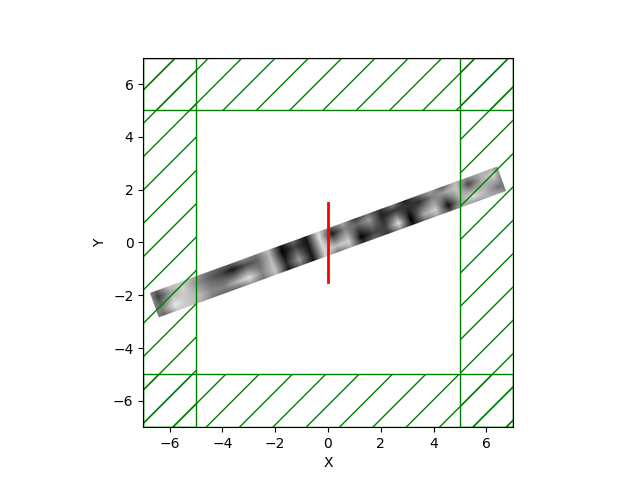
Swig and C++ routines are also in place. It also uses the existing libctl TO routines, so it's pretty efficient.
Todo:
Add support for lossy materials?