-
Notifications
You must be signed in to change notification settings - Fork 5
5.3. Taxonomy Construction
The goal of Taxonomy Construction is to organise a series of terms into a taxonomy structure where the root is the most general term within the term set and all branches are specifications from that general term. The notion of ‘general term’ and ‘specific term’ may vary from one taxonomy to another. In classical taxonomies, generality and specificity relations are characterised by relations of hyponymy and hypernymy. However, such relations could also be of type part-of or any other relation relevant to a given domain.
The taxonomy construction algorithm receives as input a set of concepts C, in which each c ∊ C is represented by a label tc (also called, a term). A taxonomy, T=(C,⊑), is then defined as a partial ordering of a set of concepts, C, satisfying the following constraints
- (Reflexivity) c ⊑ c ∀ c ∊ C
- (Antisymmetry) c ⊑ d and d ⊑ c if and only if c = d ∀ c,d ∊ C
- (Transitivity) c ⊑ d and d ⊑ e implies c ⊑ e ∀ c,d,e ∊ C
- (Unique parent) if c ⊑ d and c ⊑ e then d ⊑ e or e ⊑ d ∀ c,d,e ∊ C
- (Single root) There is some element r ∊ C such that c ⊑ r ∀ c ∊ C
Taxonomy Construction Pipeline

The task of taxonomy construction involves constructing a taxonomy from an input set of concepts, what is done in two stages (Figure above):
-
Pairwise Scoring: For each distinct pair of concepts, c,d ∊ C, we attempt to estimate the probability, p(c ⊑ d).
-
Search: Based on the probability scores given by Pairwise Scoring, we define a likelihood function f(T) that represents how likely a given structure of concepts represents a taxonomy for the set of concepts provided. Then, we use a search mechanism that attempts to find the taxonomy that maximizes the value of the likelihood function.
Pairwise scoring is accomplished by using a supervised learning setting. A SVM (Support Vector Machine) classifier is trained using: vectors representing each pair of concepts (c,d) as input, and an available taxonomy construction dataset (e.g. TexEval) in the relation between (c,d) are labelled as either +1 if c is marked as a child concept of d or -1 otherwise. This probability estimation provided by the classifier for the class +1 is then given as the estimate for p(c ⊑ d).
Saffron contains four sets of features used to perform pairwise scoring: string-based, frequency-based, word embeddings, and lexical features.
String-based features are based only in the labels of two concepts:
-
Inclusion: This feature verifies if a label is contained within another label. It is calculated as follows:
- +1 if tc ⊂ td, i.e. if the label c is entirely contained within the label for d. For instance, the label “person” is included within the label “american person”;
- -1 tc ⊃ td, if the converse is true (d is contained in c); and
- 0, if neither label contains the other
-
Overlap: This feature represents how many words are shared between two labels. Note that these words do not need to form a sequence, e.g. they can appear one at the beginning of a 3-words label and the other at the end. It is calculated by:

- Longest Common Subsequence: This feature measures the longest subsequence shared by two labels as follows:

Frequency-based features take into consideration the frequency to which concept labels appear in the overall text dataset.
- Relative Frequency: This feature measures the relative difference between the frequency of two concepts appearing in the dataset. Let f(c)denote the frequency of a concept c appearing in the dataset, the relative frequency between concepts two concepts is calculated as follows:

- Topic difference: This feature measures the difference in the distribution of two concepts. Let D(c)denote the number of documents in which the concept c appears, the topic difference between two concepts is given by:
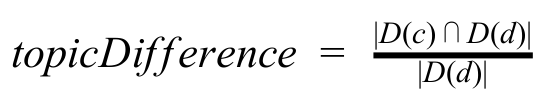
Word Embedding features provide a metric that represents the relationship between two concepts based on the relationship between their word embeddings.
Saffron uses GloVe vectors for each word and for each concept c it derives a vector vc based on the concept’s label. There are multiple ways of constructing a vector from a multi-word expression, the features available in Saffron are:
- SVD Average: We use the average value of each word vector for the term vector
- SVD Min-Max: We construct a vector whose element consists of the element-wise minimum and maximum of each word vector. This constructs a vector of double the length of the original embeddings
In order to get the relationship between two concepts we use singular value decomposition to deduce a non-symmetric function that calculates the relation between two pairs of word embeddings (For more details see Sarkar et al (2018)). The relationship is then calculated as

where the required matrix A is calculated based on existing taxonomies as described in Sarkar et al (2018).
Lexical features use existing taxonomies to infer the relationship between two concepts.
In its current version, Saffron only works with WordNet, a lexical database for English. In order to extract a taxonomy from it we extract all word pairs v,w where v ⊑ w (v is marked as being a hypernym of w). We also calculate the transitive closure of the WordNet hypernym graph, that is if v ⊑ w in WordNet and w ⊑ x, then we include that v ⊑ x in our extracted taxonomy from Wordnet.
Based on the taxonomy extracted from Wordnet, the two features for pairwise score available in Saffron are:
-
Complete Hypernyms: This feature verifies if there is any hypernym relationship between two concepts c and d in Wordnet, provided their labels tcand td respectively. It is calculated as follows for a pair of concepts c,d:
- +1, if tc ⊑ td in Wordnet;
- -1, if td ⊑ tc in Wordnet; or
- 0, otherwise
- Word Hypernyms: This feature verifies if any word wc∊tc in concept_ c_ is in a hypernym relationship with any word wd∊td in concept d in Wordnet. The score for each word pair is calculated using the Complete Hypernym method. The final score is then given by:
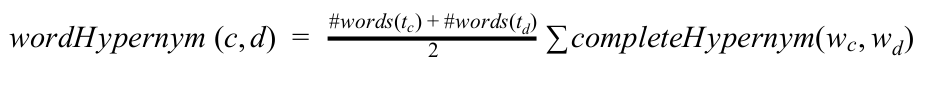
For Pairwise Scoring, Saffron uses LibSVM, a library for support vector classification. To train the classifier, we use already existing taxonomies from TexEval as the training corpus. To create a standard classification problem where we have a label of +1 if c is marked as a child concept of d and -1 in all other cases. As the negative class sample is very large we perform negative sampling, that is we take a random selection of pairs from the negative class that is in a fixed ratio, to reduce the amount of input to the classifier. Next, we feed the resulting problem to LibSVM and train a classifier.
We apply the classifier by using the probability estimation in LibSVM and return the probability that the class is +1 as p(c ⊑ d).
Saffron has three types of likelihood score based on different methods: Transitive, Non-Transitive, and Bhattacharyya-Poisson.
For this we first need to define the likelihood scoring of a taxonomy T. The obvious score would be
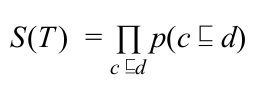
so that the multiplication of all probabilities of a completely accurate taxonomy is equals to 1 whereas any inaccuracy in the relation between concepts leads to a smaller score until arrive at 0.
Or equivalently (taking logs):

In practice, the transitive score does not work well since it is maximized by taxonomies for which there are as few as possible pair of concepts c,d such that c ⊑ d. The most trivial case is when a taxonomy is composed only by a single root concept and for which each other concept is a subconcept of only the root concept. As such, the taxonomies that are constructed from maximizing the above score tend to have a very large number of average children. In order to avoid that, we consider the set of direct children, which we denote c ≤ d should satisfies the following:
c ≤ d implies c ⊑ d c ⊑ d implies there exists e such that c ≤ e and e ⊑ d For all, c ≤ d there does not exist e, e ≠ d, e ≠ c, such that c ≤ e and e ≤ d
Based on these new constraints, the likelihood score would be:

This new likelihood score produces much better taxonomies as it is possible to show that for a set of N concepts, there are N-1 pairs c,d with c ≤ d.
Despite the improvement given by the previous likelihood function, it is still often the case that the taxonomy does not reflect the proper relations between concepts. In order to address this, we observe the number of children contained by each node in the graph. Let nc denote the number of concepts in a taxonomy that have exactly c children, if the graph were to be constructed in a truly random fashion we would expect that nc is distributed according to the binomial distribution, i.e.,

As expressed previously, there are N - 1 direct children in a graph so that p = (N - 1) / N2. As is common practice, we use the Poisson distribution as an approximation, so

This approximation allows us to vary the average number of children (λ). However the constraints on what constitutes a taxonomy (see definition of taxonomy in Section about Taxonomy Construction Algorithm) fix this value to very near 1 and we wish to vary this in order to control the taxonomy’s structure. We thus ignore the leaf nodes in the taxonomy (i.e., we ignore n0).
In order to measure the similarity of the candidate taxonomy with the theoretical value we use the Bhattacharyya distance which measure the similarity of two (discrete) probability distributions p and q as:
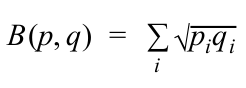
If we compare this to the actual child counts in a taxonomy we can score a taxonomy as follows:
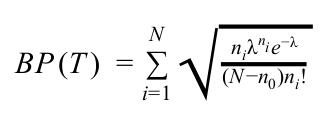
This is interpolated with the previous metric to score a taxonomy as
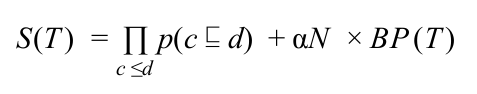
In the search step, a search algorithm is used to navigate the space of probabilities p(c ⊑ d) in order to find the structure of relations between concepts that has highest likelihood to be a taxonomy. This likelihood is represented by a scoring function f(T). The candidate taxonomy T, found by the search mechanism, containing the highest value of f(T)is given as the result for the Taxonomy Construction algorithm.
Saffron enables two types of search methods:
-
Greedy: In this method, provided the pairwise scores for all concept pairs, the pair that has the maximal score for p(c ⊑ d) is added as c ≤ d. This process is repeated until a full taxonomy is constructed, that is we take pairs c ≤ d that satisfy the first four axioms of the taxonomy (reflexivity - unique parent) until the final axiom is satisfied (single root), which means the taxonomy is complete.
-
Beam: Different from the Greedy method, where only a single partially constructed taxonomy is maintained, this method keeps a list of the top scoring possible solutions. This list (also called beam) is of a fixed size, thus the addition of a new partial solution may cause an existing solution to be dropped. Complete solutions are stored in a separate beam and the algorithm proceeds until it has considered all possible pairs of concepts and returns the highest scoring complete solution found.
This resource has been funded by Science Foundation Ireland under Grant SFI/12/RC/2289_P2 for the Insight SFI Research Centre for Data Analytics. © 2020 Data Science Institute - National University of Ireland Galway