-
Notifications
You must be signed in to change notification settings - Fork 3
B_Numeros binarios con Signo
Para poder interpretar si un número es positivo o negativo, se debe conocer con anticipación el tipo de representación que se está usando.
Podemos tener varias formas de representar números con signo:
- Convención "Signo-Magnitud". El número tiene una magnitud y el signo es representado con un 0 (+) o un 1 (-) en el bit más significativo ( a la izquierda).
- Convención del "Signo por Complemento (Complemento a 1 o Complemento a 2)" donde se representan los números negativos con el complemento del número positivo.
Ejemplo, para representar el -11 con 8 bits se puede hacer siguiendo las distintas
convenciones:
11 en binario es (00001011)
- Signo-Magnitud => 10001011
- Signo con Complemento a 1 => 11110100
- Signo con Complemento a 2 => 11110101
La representación "Signo-Magnitud" se usa en aritmética ordinaria pero no es ágil para la artimética del computador al tener que manejar por separado el signo y la magnitud. El "Signo con Ca1" raramente se usa para operaciones aritméticas, es útil para operaciones lógicas.
Vamos a realizar las siguientes operaciones utilizando la representación del "Signo con Ca2".
Si usásemos "Signo-Magnitud" en caso de ser un número positivo y otro negativo, necesitaríamos comparar las magnitudes para saber después de realizar la resta que signo predominaría.
Usando representación de los números negativos en modo Ca2 no se necesita comparar y las operaciones de suma resultan correctas con el signo incluido.
Para sumar dos números en caso de haber uno negativo, se debe calcular el Ca2
del número negativo y luego realizar la suma. En caso de que el resultado sea
negativo, este estará expresado en Ca2.
Ejemplos:
+3 00000011
-3 11111101 ( Ca2 de 3 )
--------------
0 00000000 Cualquier acarreo del bit de signo es descartado
+4 00000100
-6 11111010 ( Ca2 de 6 )
------------
-2 11111110 en Ca2 --> 00000001 + 1 = 00000010 ( 2 )
-4 11111100 ( Ca2 de 4 )
-6 11111010 ( Ca2 de 6 )
-----------
-10 11110110 ( Ca2 de 10)
Es importante para obtener un resultado correcto, asegurarse, que el número de bits sean suficientes ya que si sumamos 2 números de "n bits" y el resultado de la operación es un número de "n+1" bits estaremos produciendo un "overflow" obteniendo un resultado incorrecto.
A (minuendo) - B (Substraendo) = C ( Resto o diferencia)
- Los números negativos se trabajarán en Ca2.
- Calculamos el Ca2 del "Substraendo" y lo sumaremos al "Minuendo", esto se hace porque una operación de resta se puede convertir en una suma si el signo del "Substraendo" se cambia ( con el Ca2 se cambia su signo. Ejemplo: (+A) - (+B) = (+A) + (-B); (+A) - (-B) = (+A) + (+B)...
- El acarreo del bit de signo se descarta.
Esto nos permite usar el mismo hardware para hacer sumas y restas lo único que hay que hacer es trabajar los números negativos en Ca2, al substrayendo aplicar el Ca2, en todos casos se realizarán sumas y el resultado si es negativo siempre estará expresado en Ca2. Siempre será necesario interpretar de un forma u otra los resultados en función de que estemos trabajando con números con signo o sin signo.
Ejemplos: 4 - 10 = -6 00000100 ( 4 en binario )
+(11110110) (-10 en Ca2)
----------
11111010 ( -6 en Ca2)
-3 - (-2) = -1 11111101 ( -3 en Ca2)
+ 00000010 ( Ca2 de -2 --> 2)
--------
11111111 ( -1 en Ca2 )
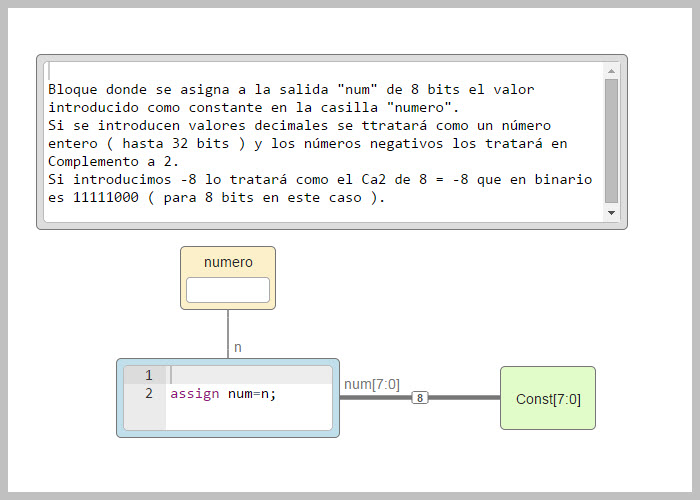
¿Cómo trata IceStudio un número introducido como constante? Se crea un módulo llamado "Const_8bits-ice" que maneja número de 8 bits donde se puede introducir un valor constante y se verá que si no se especifica el tipo de dato introducido y se introduce un número negativo como -8,este lo tratará en Ca2 y así operará con él.
En la siguiente figura mostramos el bloque realizado para introducir un valor constante:
Aquí vemos un ejemplo de su uso introduciendo el valor decimal -8:
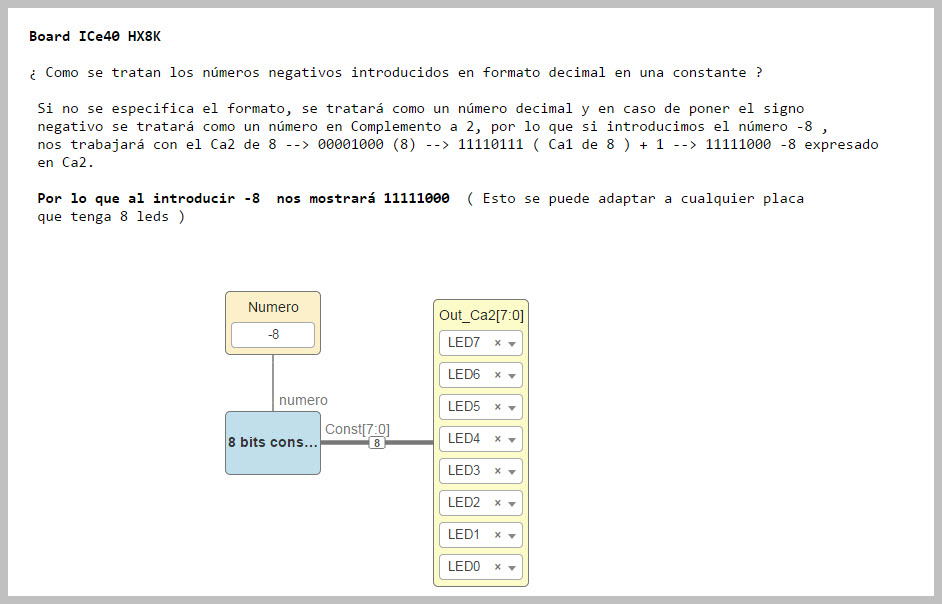
Los números positivos los tratará como números binarios puros sin convertir. Vemos que IceStudio y el Hardware usado ya es capaz de entender y convertir los números negativos a Ca2 para trabajar con ellos en forma de Ca2. (Este caso los trata como números de tipo entero y este tratará los números negativos en Ca2)
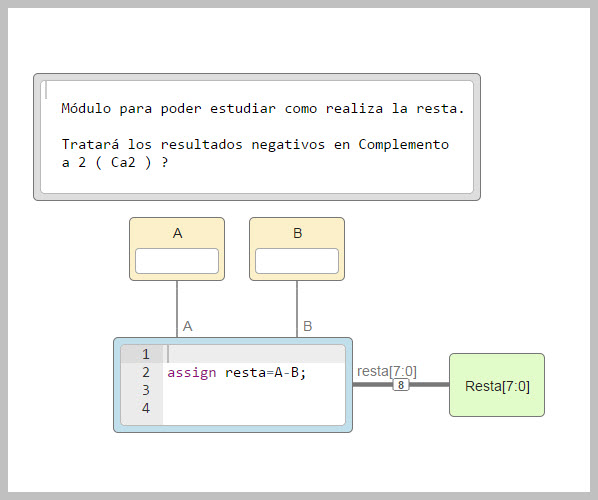
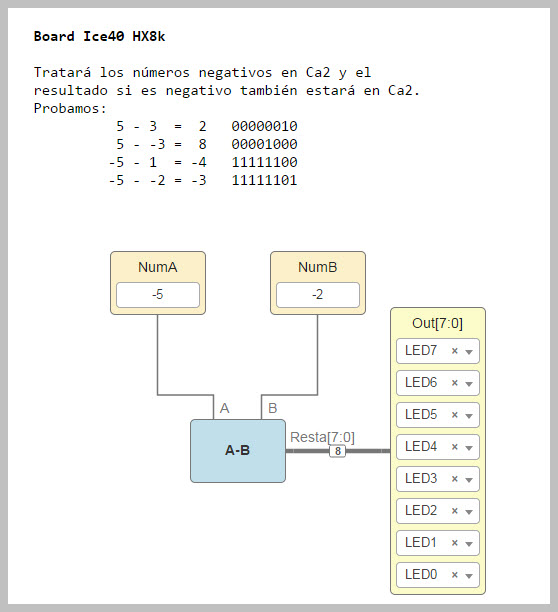
Ahora creamos un módulo donde se realiza la resta de dos valores constantes introducimos y usaremos este en un ejemplo para ver que el resultado de la resta cuando es un número negativo es tratado en Ca2 y los resultados positivos como números binarios tal cual.
Módulo de la Resta: