-
Notifications
You must be signed in to change notification settings - Fork 72
Planning Approach
Here we introduce two major abstractions which build upon the framework of Bak Constraint Satisfaction and the related work of Simple Temporal Problems (Networks). The first is the notion of an Object and the second is the notion of a Token. Before discussing Objects and Tokens in depth, we mentions some particularities concerning variables in EUROPA.
Values that need to be represented to describe the problem domain and over which we may want to specify constraints.
The things we wish to describe and refer to in a domain are considered Objects. As in the case with object-oriented analysis and design, one can seek out the nouns in any domain description to find likely objects. In a Mars rover example, we might consider the satellite, the camera, and the attitude controller (which orients the robot for taking pictures) to be objects. Objects have state and behavior. For example, a camera can be:
- off,
- ready, or
- taking a picture.
An attitude controller can be:
- pointing at a position, or
- turning from one position to another.
An object is an instance of a class. In EUROPA we model using the abstraction of a class to speak about all instances having certain properties of state and behavior. In order to describe such state and behavior we build on the formalism of first order logic.
A predicate defines a relation between objects and properties. In EUROPA, we define such relations between variables whose domains are sets of objects and sets of properties. For example, we might use a predicate Pointing(a,p) to indicate that a rover's attitude controller a is pointing at position p. Note that a is a variable which may have a number of possible values in a problem with multiple satellites. Similarly, p is a variable whose values are the set of possible positions. In a grounded plan, single values will be specified for each variable as we saw in the case of a solved Bak Constraint Satisfaction.
In general, is is not sufficient to state that a predicate is true without giving it some temporal extent over which it holds. Predicates that are always true can be thought to hold from the beginning to the end of time. However, in practice, the temporal extent of interest must be defined with timepoints to represent its start and end. So we might want to write Pointing(a,s,e,p) to indicate that the attitude controller a is pointing at position p from time s to time e. In fact, this pattern of using such predicates to describe both state and behavior of objects is so prevalent in EUROPA that we have introduced a special construct called a Token which has the built in variables to indicate the object to which the statement principally applies and the timepoints over which it holds. In EUROPA, all predicate instances are Tokens.
A Token is an instance of a predicate and is defined over a temporal extent. Every token has five built-in variables:
- start: The beginning of the temporal extent over which the predicate is defined.
- end: The end of the temporal extent over which the predicate is defined.
- duration: The constraints start + duration = end is enforced automatically.
- object: made. The set of objects to which a token might apply. In a grounded plan each Token applies to a specific Object, reflecting the intuition that we are using Tokens to describe some aspect of an Object (i.e. its state or behavior) in time. However, in a partial plan, the commitment to a specific object may not yet have been made.
- state: Tokens can be ACTIVE, INACTIVE, MERGED, or REJECTED. The state variable captures the token's current state and its reachable states through further restriction. See the Token State Model discussion below for details.
As we have noted, Tokens describe some aspect of an Object in time. Objects thus may have many Tokens in a plan in order to describe their state and behavior throughout all points in time of the plan. Within this general framework, we note a few particulars:
- Static Facts: Classes without predicates lead to Objects without Tokens. This arises where an objects state or behavior is independent of time. For example, a domain may have a set of locations and/or paths for which there is nothing more to say than that they exist.
- Timelines: Often objects in a domain must be described by exactly one token for every given timepoint in the plan. Such objects are so common that we provide a special construct in EUROPA to extend these semantics to derived classes. Any instances of a class derived from a Timeline will induce ordering requirements among its tokens in order to ensure no temporal overlap may occur among them. See below for further discussion.
- Resources: Metric resources, e.g. the energy of a battery or the capacity of a cargo hold, are objects with an explicit quantitative state in time and with a circumscribed range of changes that can occur to impact that state i.e. produce, consume, use, change. These changes are captured as tokens. Resources are such a common requirement for EUROPA users that special constructs are also provided for them. Instances of classes derived from a Resource will induce ordering requirements on their Tokens in order to ensure that the level of the resource remains within specified limits.
TODO (there was a stub in the old doxygen docs for this)
It may be sufficient to maintain only a partial-order among tokens. However, it is often the case that tokens represent states and actions of a single object in the system. Such tokens are typically mutually-exclusive. EUROPA uses a Timeline structure developed in (11) to concisely capture system components whose behavior is described over time in this manner.
For example, consider the tire-world domain. The tire was located in the trunk with the predicate tireLocated(Trunk) and located on the ground with the predicate tireLocated(Ground). Clearly, the same tire cannot be in both places at once. A Timeline provides a simple method for aggregating the statements about a tire such that they are mutually exclusive.
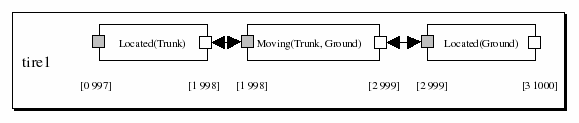
Figure 1: A Timeline for a Tire
Figure 1 illustrates how a Timeline can be used to describe the whereabouts of a tire. The tire is an object in the tire-world represented as a timeline. It has predicates associated with it which can describe its states and actions over time. The predicate names need not contain the tire prefix; this is now implicit since the tokens are assigned to a specific tire instance (i.e. an instance of a Timeline). While Timelines are a useful element of the EUROPA planning paradigm, they are not essential. A more general notion of a system Object can be used which does not impose restrictions of mutual-exclusion or non-zero duration. This can be important in supporting partial-order planning.
For this example, the state of the tire is specified using 3 contiguous tokens. The end and start time-points are related by an equality constraint. A Moving predicate has been introduced to cover the transition from one location to another. It takes 2 location arguments. Notice that precedence relationships exist between tokens such that they cannot overlap but the start and end times may remain flexible. To illustrate this, sample times are included. Assume a total time range of interest between 0 and 1000. In addition, tokens on Timelines have a minimum duration of 1. As a result the values shown are the most flexible possible values for the start and end of each token. There are a number of advantages of allowing this flexibility. First, the basic structure of the plan can be developed without over-committing to specific times. If it is not necessary for the tire to be on the ground at time-step 4, then a planner should not be forced to specify it. Such an approach permits a least-commitment approach to planning. Second, in many domains it is simply impossible to know in planning exactly how long an activity might take. For example, a common activity of driving a car from one point to another on a road can take varying amounts of time depending on traffic and traffic lights. In such circumstances it is more practical to express upper and lower bounds on durations which naturally lead to intervals for start and end times. In such domains, flexibility in planning aids robustness in execution.
In order for a plan to be valid, it must comply with all rules and regulations pertinent to the application domain in question. Rules govern the internal and external relationships of a token. For example, consider a parameterized predicate describing a transition from one location to another. Let the parameters be from and to. The parameters are instantiated on a token as variables whose domain of values is the set of all locations in a given problem. A rule governing an internal relationship among token variables might stipulate that a transition must involve a change in location. This can be easily expressed as a constraint on the definition of a predicate of the form: from != to. It is reasonable to further stipulate that one must be Located somewhere before a transition can occur, and one must end up Located somewhere when completed. This is an example of a rule governing an external relationship among tokens. It specifies a requirement that tokens of the predicate Located precede and succeed tokens of the predicate Moving.

Figure 2: Internal and external relationships from rules on Moving
Figure 2 illustrates the entities and relations involved in specifying such a rule on a Moving predicate. The token on which the rule applies is referred to as the master. Each Located token required by the master is referred to as a slave. All variables are indicated by name and their domains are expressed as intervals in the case of temporal variables and as enumerations for the remainder. Application of a rule on a token can thus cause slave tokens, variables, and constraints to be introduced.
The capability of a domain rule to cause a slave token to be created is a key vehicle through which planning occurs. Semantically, this rule imposes a requirement for supporting tokens to be in the plan in order for the master to be valid. There are 2 possibilities to consider: 1. The slave is inserted as an active token in the plan. As such, rules may be activated on the slave, and it may consume resources. 1. The token is merged with a matching token already in the plan. Once a slave is merged, the requirement it represents are considered satisfied. The process of merging passes on all restrictions imposed on the slave to the active token upon which it is merged. Merging a token requires finding a target active token that is compatible with the inactive token. For an active token and an inactive token to be compatible requires that they are instances of the same predicate and that no intersections between corresponding variables are empty. The effect of merging is illustrated in Figure 3.
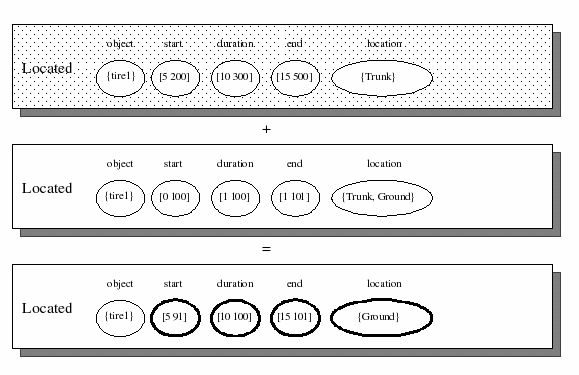
Figure 3: Merging an inactive token on an active token. Domain restrictions occur in highlighted variables of active token.
On creation of a token, where the commitment has not been made yet to activate or merge the token, the token is said to be inactive. There is a nuance to the state model for tokens which relate to the mode of its creation. If the token is allocated explicitly by an external actor, rather than internally through rule firing, it may include the state rejected indicating the planner is permitted to reject the token. A valid plan can include rejected tokens. This typically arises where the token represents a goal that is preferable to achieve but not mandatory. This state is not reachable for slaves since that would imply selective adherence to the domain model. Figure 4 presents the state transition diagram for token states relevant for planning. The transitions are operations on a partial plan which can decide an outcome for an inactive token. As operations which may arise in search, they must be reversible during backtracking. The cancellation operations in each case are also shown.

Figure 4: Token states and transitions for planning.
The state of a token is embodied with a 5th and final built-in variable referred to as the state variable. The planner states are values in the domain of this variable {MERGED, ACTIVE, REJECTED}. The INACTIVE state is captured by the variable being unbound. If a value is removed from the domain, that state will not be reachable. For example, when a slave is created via a rule, the REJECTED value is removed from its state variable.
This page has presented the main elements of the EUROPA planning approach. They are: 1. Temporally scoped predicates (a.k.a. Tokens) to represent states and actions in time. Note that tokens do not discriminate between state and action. 1. Constraints to describe relationships among tokens. This provides an expressive method of describing interactions among tokens in the context of Temporal Planning. 1. Timelines as a concise abstraction to express the evolution of state and behavior for a system component. It provides semantics of mutual exclusion sequencing in time. Other core abstractions are available in EUROPA for handling metric resources. 1. Domain rules to describe internal and external relationships on and between tokens respectively. Rules are applied to active tokens (master tokens) referred to as masters and typically produce inactive tokens (slaves) which are a key vehicle through which the planning process evolves. The rule structure in EUROPA differs from the more restrictive commitment to preconditions and effects in classical planning which prohibits durative actions and disembodied effects (i.e. effects which may not occur until some temporal distance after the end of the action). 1. Token States which are the basis of planning operations on a partial plan.